![]()
1.エンジニアにおける実験計画法(Design Of Experiments)
エンジニアにおける実験計画法の取り組みには幾つかのパターンがあり、大きく分けると実験手法として手慣れた範囲にあるのかとそうでないのかに分かれる。前者では更に上があり実験計画法も選択肢の一つではあるが、品質工学や数値解析・シミュレーション(CAE)などを選択する環境も整っているというレベルがある。後者も同様に実験計画法を一部取り入れているというレベルから、一元配置法はおろか分散分析を試みたことがないというレベルまであり、果たしてエンジニアの何れが少数派であろうか。実験計画法自体は既に枯れた手法ではあるものの、エンジニアが実施する実験方法に占める割合は然程大きくはなく、旧態依然の決め打ちによる任意因子と水準による実験が未だに多いと思われる。前者のエンジニアに対しては管理人の出る幕ではないが、ここでは後者のエンジニアをサポートする目的で書くつもりである。決め打ちによる任意因子と水準による実験を繰り返すことの最大の弊害は、「要素データの蓄積が全くできない」の一点に尽きる。旧態依然の実験検証でもその場のブレークスルーは可能である(設計値を決定できる)が、そのデータを次の製品設計に活用できるかというと殆どの場合はできず、もう一度検証しなければならないことが多い。これは次の新製品ではC/Dや機能改良などのために設計因子水準が旧製品と異なっている場合が多く、旧製品の検証データがそのまま適用できないからである。
2.従来の実験方法の問題点
下図の特性要因図に示すように製品の特性(Y)は、一般的に多くの要因(因子:Xi)の影響を受ける。しかし限られた時間内に全ての組合せ実験をすることは容易ではなく、YとXiの関係を明らかにしたいとき往々にして以下のように実施されることが多い。要因と因子は意味するものは同じであるが、前者が全般的なものを指すのに対して後者は個別的(若しくはより具体的)なものを指す。
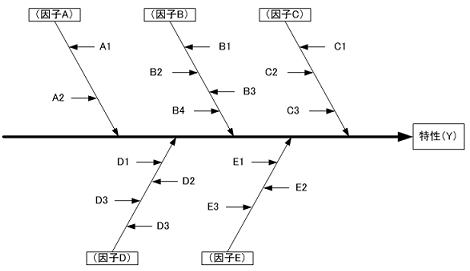
●実験方法1
1因子毎に水準を振りその実験結果から因子水準を決定し、全ての水準が決定したらそれを最適水準(この例ではA2B1C1D2E1)とする方法。
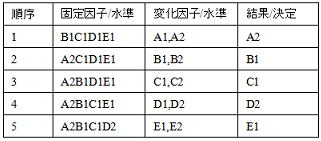
●実験方法2
過去の知見あるいは経験則から予め影響が大きいと思われる因子のみ(一つあるいは複数)を取上げ、残りの因子は全て固定因子とした実験結果から最適水準(この例ではA2B1C1D1E1)を決定する方法である。旧態依然の実験ではこの方法が最も多いと思われる。
何れの実験も任意因子の組合わせによる実験回数の絞り込みのため、データ取得後の統計的手法(分散分析)が適用できず全体のばらつきから因子の効果を分解(抽出)できない。敢えて言えば詳細な実験を実施する以前の暫定実験の域を出ないものである。分散分析による定量評価ができないため、特性(Y)に対し各因子(Xi)水準がどの程度影響(効果)しているかまでは判断できず、変化因子/水準の優劣はその組み合わせでのみ言えるだけで、何れかの水準が異なれば異なる結果になる可能性があり最適水準は疑わしいということになる。任意の絞り込みから得られる情報(実験結果)は限定的であり、前述したようにその場に限ればブレークスルーできる可能性は高いが、別の製品で要素データとして活かせるかは全く別の話である。従来の実験方法では要素データを蓄積することはできないことを認識すべきである。
3.実験計画法の導入目的
新(未知の)分野などにおける理論検証のための物理実験ではその安定性・再現性は絶対的なレベルが要求されるが、一方我々エンジニアが日常的に扱う技術的な課題では、実験条件を完全に管理することには限界があり一定のばらつきを容認している。実験計画法はフィッシャーが農場実験を計画遂行する際に実験をいかに合理的に行うかの手法として考案したもので、彼が行った農場実験はまさしく自然が相手であり実験条件を一定に保つことは不可能であった。つまり変動要素のある環境条件で収量の多い品種や効果のある肥料を見付ける必要性から考案されたもので、実験計画法では一定の“ばらつき”を認めていることになる。但し認めた上でできるだけ厳密に扱って、正しい結論に導こうというものである。このような考え方は産業分野への応用に非常にマッチしており、実験といえば実験計画法といっても過言ではないのだが、前述したように早く結論を得たいが為に任意の絞り込み(決め打ち)による実験も多く行われているのが実情である。
多くの要因(因子)を問題にしなければならない特性については、余程計画的に実験しないと結果の解釈が曖昧になる可能性が高く、実験計画法とは「どのように計画的にデータを取得すればよいか」、「データをどのように解析すればいいか」についての統計的方法論を纏めたものであり、従来のやり方の問題点を払拭するための統計的ツールと考えることができる。一見すると従来実験回数より多くの実験回数をやるようにも映るが、統計理論に基づいた実験回数の絞り込みは任意因子の組合せによる絞り込みとは全く別のものである。2項における特性要因図の段階では様々な要因が関わっていることは分かるが、「どの要因(Xi)が特性(Y)にどのくらい影響を与えているか」までは分らない。実験計画法の目的は特性(Y)と要因(Xi :一つあるいは複数)の関係を客観的に明らかにすることである。
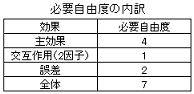
4.実験回数と得られる情報
多元配置法の実験では因子数とその水準が多くなると実験回数が飛躍的に増大する。具体的な例として2水準の因子を3,4,,,と因子数を増加させた場合の実験回数と、実験結果から得られる情報量(自由度)の配分を下表に示す。取り上げる因子数が多くなると実験回数は飛躍的に増大し、それに伴い交互作用(2因子以上)の情報量が多くなることが分かる。これは得られたデータから計算される総平方和が、各平方和(例えば3因子A,B,Cの場合:A,B,Cの主効果、A×B,A×C,B×Cの2因子交互作用、A×B×Cの3因子交互作用の7個の情報)に分解できることを示している。しかし3因子以上の交互作用は存在自体の可能性が低く、また2因子交互作用も全てを取り上げる必要性は必ずしもない。従って仮にその自由度を取り上げたとしても
F0<1.0~2.0になる可能性が非常に高く、分散分析を行う際結局誤差項にプーリングされる(誤差項の自由度が不必要に増大)ことになる。総組合せ実験は情報量は多いが不必要な情報量(自由度)が多い不経済な実験
ということになり、更には実験条件の維持管理、偶然的な変動の拡大、コスト増大、再現性の低下など抑えなければならない検討事項も多い。

5.実験回数の減らし方
技術的課題のブレークスルー初期段階では課題に関連する特性値に影響する要因は分かっていても、その特性値に何れの要因がどの程度影響(効果)しているかまでは分からない。これを明確にするには多くの要因を取り上げて特性値に関する実験を実施する必要があるが、実験回数の減らし方に特別の工夫をしない限り多元配置法(総組み合わせ)による実験となる。しかし多元配置法には実験回数が多い故の問題点があることを4項で述べた。不必要に情報量が多いとは不必要な実験を実施していることを意味しており、予め何れの組み合わせが不要か(若しくは必要最低限の組み合わせ)の判断が得られれば、それらは実験回数から外せる(若しくは必要最低限のみ実験すれば良い)ことになる。4項に述べたように3因子以上の交互作用の情報(自由度)は不要で、2因子交互作用もその必要性が全てにある訳ではなく、むしろ技術的な知見情報などから外せる(取り上げなくてもよい)自由度の方が多く、予めその分の自由度は総自由度(N-1)から差引くことができる。つまり抽出したい因子効果数(主効果と交互作用の数)を大胆(且つ慎重)に絞り込むことで、実験回数を減らすことは可能なのである。2/3水準系の主効果・交互作用の自由度は以下表の通りで、例えば以下の様に絞り込むとするなら5因子/2水準では、必要実験回数は32回→7回に減らすことができるのである。但し減らせるからと言って任意的な判断による実験(回数)の絞り込み、効果が“ありそうだ”と思われる要因に限定した実験では、情報(自由度)の外し方に一貫性がないため定量的な評価が難しく結果の信憑性も疑わしい。この際に必要な実験回数をどのような水準組み合わせで実施したらよいかを教えてくれるツールが、次項以降に述べる直交配列表である。
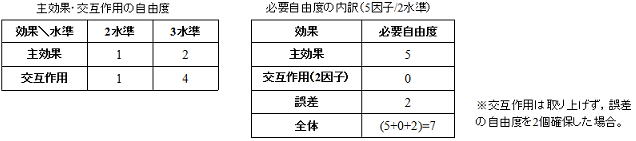
6.直交配列表
2項に述べたように必要情報量を絞り込むことで実験回数は減らせることが分かった。但し総組み合せ回数から無作為に選んでいいということではなく、その回数をどのような水準組合せで行ったらいいかの課題は残っている。この時どのような組合せで実験すればいいかを教えてくれるツールが直交配列表で、以下に直交配列表による実験計画法の特徴を示す。
a)多くの因子に関する情報を少ない実験回数で得られる。
b)必要最低限なルールのみで機械的に因子の割り付けが可能である。
c)取上げた因子の主効果と交互作用の有無を同時に検定できる。
d)2因子交互作用は予め「検討すべき組合せ」と「無視できる組合せ」に区分する必要がある。
e)データ解析は基本的にANOVA1,2と同様であり容易である。
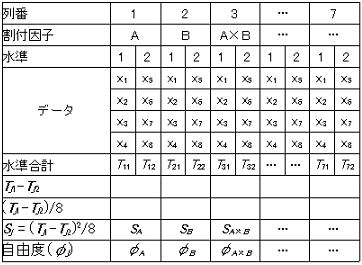
我々が通常行っている実験規模では主効果(2~4水準)が5個前後割付けられれば十分であり、抽出したい交互作用(2因子)の数にもよるが殆どの場合は以下の直交配列表の範囲で十分カバーできよう。直交配列表は“L”とそれに続く添え数字で表すことが一般的で、2水準系ではL#(2n)、3水準系ではL#(3n)のように表示される。Lの添え数字(#)は直交表の行数を表しており、この値が直交配列表の大きさ(実験規模)となりnは割り付け可能な列数になる。この内2水準系のL16直交配列表は割り付け列が15列と比較的多く、2水準以外の3/4水準因子を一つあるいは二つ取上げても余裕があり最も汎用性が高い直交配列表といえる。なお適用される水準系以外の因子水準を割り付ける方法については後で述べる。

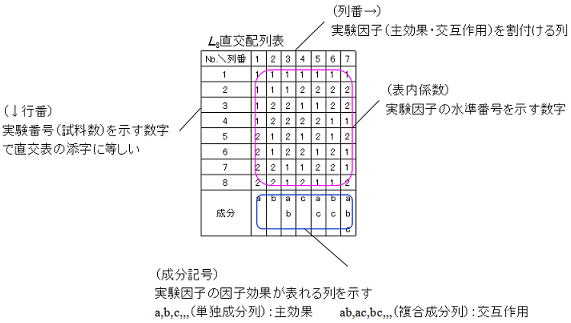
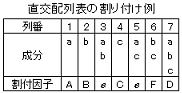
7.直交配列表の構成
直交配列表の“行”(row)と“列”(column)には明確な定義があり、その構成要素は各直交配列表毎に決められており、下図に代表的なL8直交配列表の構成(各諸元)例を示す。
8.因子の割り付け方法
8.1因子水準表の作成
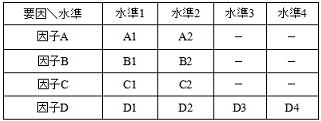
実験目的を十分達成できるかはこの段階で決まると言っても過言ではなく、事前に特性(Y)に関連する情報を十二分に調査し特性に影響があると考えられる要因(Xi)をリストアップする。その中から影響度の大きさ、水準管理の難易度、実験コストなど保有している知見情報を整理熟考した上で因子を選定する。6項に示すように直交配列表の標準水準数は2~4水準であり、因子水準を2~4水準の範囲で設定すると適用できる直交配列表の選定が容易となる。計量的な因子では水準数を多く取った方がより良い条件を見付けやすいが、闇雲に多水準にすることは実験回数の増大に繋がるだけである。水準設定の重要なポイントとして、各因子水準にベンチマーク水準(例:A1B1C1D1)を入れることが上げられる。ベンチマーク水準における特性(Y)の値は既に既知の場合が殆どであるが、新たに実施する実験において再現性が保たれているかの確認も重要であり、ベンチマーク水準を取り入れることは常套手段と考えて欲しい。全てが決定したら以下に示すような因子水準表を作成する。
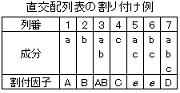
8.2成分記号による割り付け
実験をどのような水準組合せで行うかを決定する行為を“割り付け”といい、直交配列表を用いた割り付け方法には下図に示すような“線点図”を利用する方法と、直交表の“成分記号表”による方法がある。取り上げる因子数が多かったり検討すべき交互作用が多い場合には前者が便利であるが、エンジニアが実施する通常の実験規模の範囲では、後者でも割り付けは十分可能である。
1)標準水準数で交互作用を取り上げない場合
取り上げた因子水準数(2水準又は3水準)と必要自由度から直交表の種類と大きさが決定することは、全てのケースで基本となる。この場合の必要自由度は(主効果数+誤差)となり、主効果数は取り上げた因子数でそのまま決定するが問題は誤差の自由度である。分散分析を実施する上では誤差の自由度は最低1個は確保する必要があるが、統計的な観点(検定の検出力と推定精度)では誤差の自由度はできるだけ大きくした方がよく、誤差の自由度は原則として2個以上は確保したい。先ず主効果を単独成分(成分記号が1個の列)の列から順に割り付け、単独成分の列が無くなったら原則として成分記号数が多い列から割付ける。最後に何も割付けられなかった列は誤差(e)に指定する。例として2水準系で5因子(A,B,C,D,F))取り上げた場合の割り付け例を以下に示す。2水準系で必要自由度が7個であることからL8直交配列表(列数が7個)を選択し、因子列の係数から以下の8個の水準組み合わせにより実験を実施することになる。
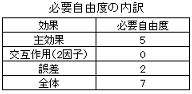
2)標準水準数で交互作用を取り上げる場合
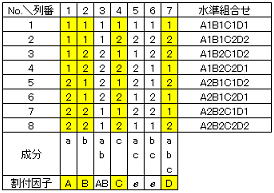
交互作用を取り上げる場合は交互作用を構成する主効果2個と交互作用1個の計3個の列が必要になり、それには直交配列表の単独成分記号の列2個と、その二つの成分と掛け算のルールが成立する列の計3個の列を選択し、先ず取り上げたい交互作用の主効果を単独成分の2個の列に割り付け、次に主効果を割り付けた成分記号と掛け算のルールが成立する列に交互作用を割り付ける。交互作用を取り上げる行為自体はどの列から抽出するかを特定することであり、主効果の割り付け自体は取り上げない場合と変わらない。残りの主効果を単独成分の列から順に割り付け、単独成分の列が無くなったら原則として成分記号数が多い列から割付け、
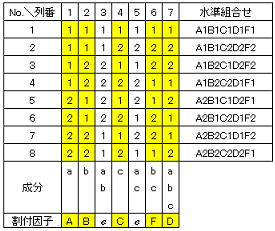
何も割付けられなかった列は誤差(e)に指定する。例として2水準系で4因子(A,B,C,D)を取り上げ、交互作用としてA×Bを取り上げた場合の割り付け例を下図に示す。この例では交互作用(A×B)の主効果(A)を第1列、主効果(B)を第2列、交互作用(A×B)を「二つの成分と掛け算のルールが成立」する第3列に、それぞれ割り付けられている。これらの関係が成立する列は他(例えば第2列、第4列、第6列)にもあり、何れを選択するかで水準組み合わせ自体は変わるが、各因子の効果は同様に抽出可能である。2水準系で必要自由度が7個であることからL8直交配列表(列数が7個)を選択し、因子列の係数から以下の8個の水準組み合わせにより実験を実施することになる。
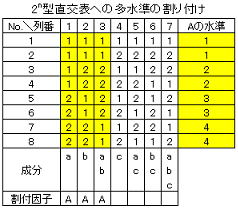
3)多水準がある場合
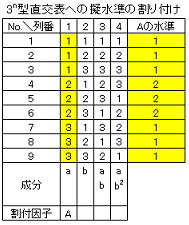
一般的には2n型直交配列表(L8,L16など)に4水準の要因を割付ける方法である。つまり取り上げた因子の内複数個(通常は1個又は2個程度)4水準の因子があり、他は全て2水準という場合である。4水準の自由度は3で2n型直交表の各列の自由度は1であるから、自由度3に対応するためには3個の列を用いて割り付 ければよいが、その列(3個)は主効果と交互作用成分が掛け算のルールが成立する必要がある。下の例では主効果と交互作用が掛け算のルールが成立する第1列~第3列を選択し、因子Aを割り付けたことになる。ここでのポイントは因子Aの実験水準の割り付け方法である。表内の係数に3,4が存在しないため、割り付けた3個の列から任意の2個(この例では第1列と第2列)を選択し、その係数の組合せ(4通り)から因子Aの水準を下表のように決定する。なお割り付け列あるいは任意選択の列番が異なればAの水準も異なることになるが、得られる結果には全く影響しない。
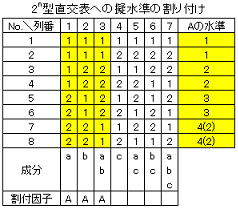
4)擬水準がある場合
2n型直交表(L8,L16)に3水準の要因を割付ける場合と3n型直交表(L9,L27)に2水準を割付ける場合がある。いずれの場合も元の水準に対してダミー水準を充て元の水準を擬水準と呼ぶことからこの名がある。2n型直交配列表に3水準の因子を割り付ける際の基本的な考え方は多水準(4水準)と同様であるが、3水準を割り付けた後に水準が一つ余るため1~3水準の内最も重要な水準を繰り返して割付ける。割り付ける列の選択は多水準の場合と同様に主効果と交互作用成分が掛け算のルールが成立する3個の列を選択し、割り付けられた3個の列から任意の2個の列の係数組合せから以下表のように指定(擬水準A4の代わりにダミー水準A2を指定)する。
3n型直交表に2水準の因子を割り付ける場合は列の自由度(2個)の関係から一つの列にそのまま割付け可能で、余った水準は1~2水準の内最も重要な水準を繰り返して割り付ける。
主効果の割付け(単独成分列)と同様に任意の1列を選択し、選択した列の係数から下図のように指定(擬水準A3の代わりA1を指定)する。
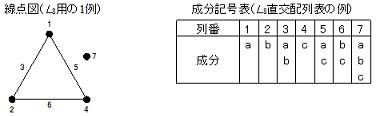
8.3線点図による割り付け
取り上げる因子数が少ない、多水準・擬水準の設定が1~2個の場合は直交配列表の成分記号でも十分割り付けは可能であるが、多水準・擬水準の数が3個以上、考慮する交互作用の個数が多い場合は少し機械的な工夫が必要になる。線点図はこのような時に便利なツールで、その代表的な例としてL8直交配列表とL16直交配列表の線点図を示す。線点図は因子(主効果)は点、点間を結んだ線分は交互作用に対応しており、主効果と交互作用の関係にある列が視覚的に分かるようになっている。
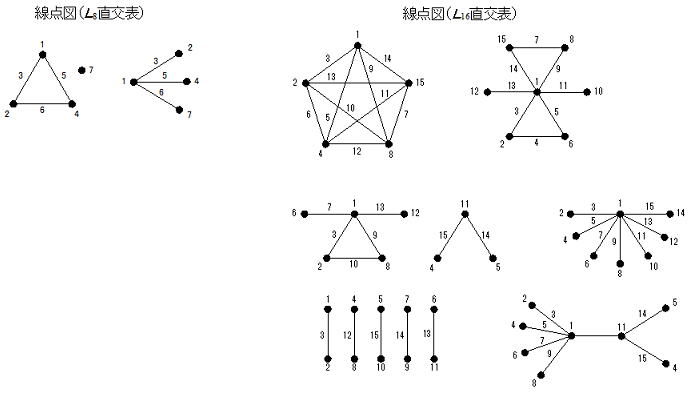
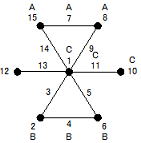
線点図による割り付けにおける標準的な手順は、先ず評価者が知りたい情報(主効果、交互作用、多水準など)を基に必要な線点図を作成(この時点では線点図に記載されている列番号はない)し、次に必要とする自由度に対応した直交配列表の線点図に照合させ列番号を確定させる手順になる。但し慣れてくるとエンジニアが扱う一般的な実験規模の範囲では、必要な自由度に対応した直交配列表の線点図に直接書き込んでも問題はなく、実際管理人は必要な線点図を作成したことは殆どなかった。下図はL16直交表に多水準(主効果と交互作用が掛け算の関係が成立する3列を選択)を3個を割り付けた例であるが、交互作用を取り上げなければ誤差項の自由度(2個)と複数の主効果を割り付けることができる。
9.2水準系直交配列表における分散分析
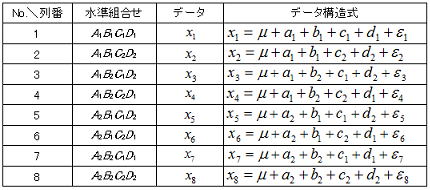
9.1データの構造
L8直交表に4因子を割付けた場合のデータ構造式における因子効果と誤差の振舞い例を下表に示す。ここで各因子効果にはANOVA1,2で述べたと同様に以下の制約条件がある。

データの構造式と要因の制約条件から例えば因子A1の効果は“A1水準の平均と一般平均の差”と定義できるのでその効果は以下の式で推定できる。構造式はそれぞれ誤差(εi)を含むので値は推定値である。同様にA2水準の効果を求めてみると制約条件と一致することが分かる。平方和は効果の2乗和で計算できるので以下のように置き、A1,A2水準で各4回実験が行われることから因子Aの平方和SAは以下のように求められ、この式が分散分析を行う際の基本的な考え方となる
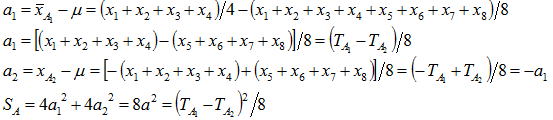
9.2平方和の計算方法
平方和を求める基本式は9.1項に示した通りなので直交配列表の全ての列にこの式を当てはめればよく、下表にL8直交配列表における計算例を示すが(水準1の合計-水準2の合計)が、全ての計算の基礎になっていることが分かる。なお多水準、擬水準、誤差(e)など複数列に同一因子が割り付けられている場合は、その因子の平方和は複数列の総和となる。
最後に以下の式により総平方和を求める。
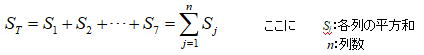
なお総平方和は以下の式によっても求められ、平方和の計算方法を実施する前にこの方法で計算しておくと、各無平方和の合計値との照合が可能になる。

9.3自由度の計算方法
列平方和に対して“列自由度”として考えることができ、2n形直交配列表の各列の自由度は1であることからこれがそのまま適用される。複数列に割り付けられている場合は平方和と同様に総和となる。 総自由度は以下の式で求められ7個となる。
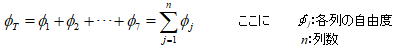
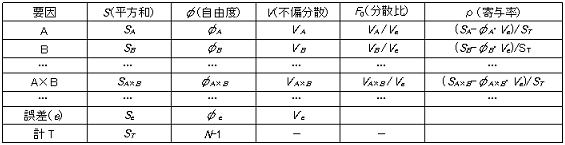
9.4分散分析表
“列平方和”と“列自由度”から割り付けられた因子の平方和と自由度を計算し分散分析表に纏める。一般的な分散分析表はF0(分散比)までの表記であるが、どの因子の平方和が全平方和に対してどのくらいの割合であるかを検討する材料として以下の寄与率を付加する。
因子の寄与率=(S*-φ*・ Ve) / ST
9.5プーリングの検討
実験計画法では多くの因子を取り上げるので、特性値に影響ない因子はできるだけ排除したい。しかし分散分析結果から「有意でない」≒「影響を与えていない」とは必ずしも言い切れない面がある。そこでF0値を考慮して「有意でない」∩「F0値がある程度小さい(一般的な判断基準:≦1.0~2.0)」因子はプーリングする。プーリングすることにより誤差項の自由度が大きくなり、検定や推定の精度が高くなる。誤差の自由度の目安:総自由度の約1/2程度
9.6分散分析後の検討
因子の各水準における母平均の推定は以下により求められる。
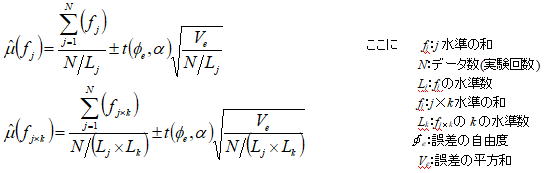
最適条件における母平均の推定について、単一因子のみの組み合わせ、交互作用が一つある場合、交互作用が二つある場合の組み合わせ例における推定方法を示す。
9.7誤差の大きさの検討
実験計画法(ANOVA1,2)にも述べてある内容であるが、再確認の意味合いを含めて重要事項なのでここでも述べるものとする。誤差分散Veはデータの構造式における誤差εの母分散(σ2)の推定量で、母標準偏差の推定量を導く値になりVeが妥当な値であるかの検討は重要である。つまり特性(Y)のばらつきの妥当性を検討する材料になり、予測された範囲に収まっている(設計の本質に依存している)かの判断は、実験担当者が技術的見地から判断する以外にないが、Veが妥当な値で且つ有意な因子は量産規模でも十分効果があると判断できる。
10.3水準系直交配列表における解析
10.1平方和の求め方
3水準系の場合は2水準系のような簡便な求め方はできないため以下の基本式を用いて計算しなければならないが、各列の平方和が割り付けられた因子の平方和に対応することは2水準系と同様である。

10.2自由度
列の自由度は、各列に3水準設定されている関係から、以下のように推定できる
![]()
11.用語の補足説明
11.1プーリング
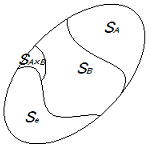
効果がないと判断される要因効果を誤差とみなし、その平方和を誤差平方和に繰り入れ同時にその自由度も誤差自由度に加えることをいう。要因配置実験では主効果はプーリングしないが、直交配列表を用いた実験では一定の基準でプーリングすることがある。例として有意でない交互作用A×Bをプーリングするイメージを下図に示す。見掛け上誤差項を大きく見積もることになり検定や推定の精度が高くなる。
なお交互作用(A×B)をプーリングしない場合は、原則として各主効果(A,B)はプーリングしない。
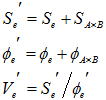
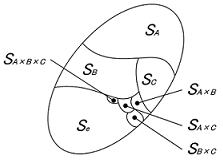
11.2交互作用
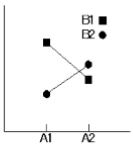
下図のように二つの要因A,Bが要因水準の違いに因り特性の現れ方が異なる傾向を示すとき、 AとBの間に交互作用があるといい“A×B”で表す。つまり要因AとBの効果はその水準組合せで決定することになり、この場合は単独の要因効果を求めても意味がない。なお3要因以上の高次交互作用は存在しないことが多く一般的には無視できるといわれている。
2因子交互作用を取り上げるかどうかは、評価者が保有している固有技術情報の範囲で決定する必要がある。管理人の経験からは機械構成品における特性値(Y)の実験では殆どの場合取り上げる必要はなかったが、勿論管理人が検証した範囲での話であり、外せると判断できる技術情報が全くない場合は取り上げることが推奨される。
11.3自由度
簡単には“データの個数”であるが、互いに自由に値を取る(独立に動ける)ことができる変数の個数をいう。 母集団からn個のサンプルを抜取り分散を推定するとき、母集団の本当の平均値は分からないためサンプルの平均値を利用して分散を推定することになる。例として下式のように5個のデータから分散を推定
した場合、この分散推定値は正しいと言えるだろうか。問題点の一つとして試料平均を用いて分散を推定している点が挙げられる。つまり今回のデータではV=2と推定されたが試料平均はサンプリングの都度ばらつきを持つ(試料平均は試行都度異なる)ため、それを基準に推定している平方和はばらつきの情報を一つ無視していることになり、この値より控えめな値になることが予測される。
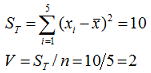
平方和Sを構成する偏差の振る舞いを考えてみよう。平均値を5に固定して下図のように箱に1個づつデータを自由に入れられるものとする。4番目までは自由に入れることは可能であるが、果たして5番目は可能であろうか。答えは勿論“否”であるがこれは平均値が束縛しているからであり、偏差はn個の値を持ってはいるもののその自由度はn個ではなく (n-1)個の情報(自由度)だと考える訳である。従って分散を求める際は平方和Sを(n-1)で割るのが正しいことになり上の値(2)より大きく推定される。
![]()

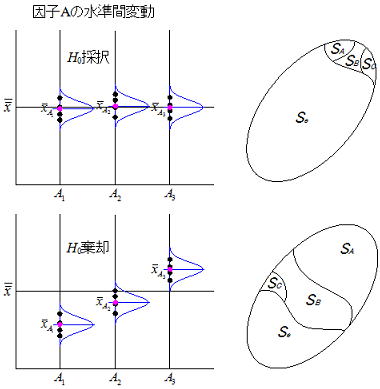
11.4誤差(項)
割付けた因子効果が全て下図のように有意でない(水準間に差がない)場合は総平方和(St)に占める誤差の割合は非常に大きくなり、対して各因子の効果が大きい場合は誤差の割合は小さくなる。誤差は取り上げなかった全ての因子変動と偶然的に発生する変動の総和であり、観点を変えるなら誤差も因子の一つとして考えればよい。説明を簡単にするために要因が一つ(一元配置)のデータ構造を考える。要因AにおけるAi水準のj番目のデータは下記式のように展開され、総ばらつきは水準の違いによるばらつきと誤差によるばらつきに分解される。
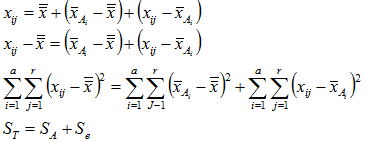
11.5要因と水準
要因は実験結果(知ろうとしている特性値)に影響を与えると考えられる事がらの総称で、“因子”と呼ぶ場合もある。要因には実験担当者が決められる(制御できる)要因と、特性に外乱(ばらつき)を与える二つのタイプがある。水準は要因をいくつかの段階(物理量としての値の違い、材料や処理方法などの違い)に分ける条件をいう。
12.纏め
直交配列表実験を一度成功させると、今までの実験は何だったんだろうと思うぐらい実験に対する考え方(見方)が変わる。我々はQC検定を取得することが目的ではないのでANOVA1,2→直交配列表実験に亘る詳細な理論を全て理解する必要はないが、実験の計画及び分散分析結果をどのように捉えればいいかについて、以下の最低限の知識は抑えておく必要がある。
a)固有技術情報をベースとした特性(Y)に影響を与える要因(X)の抽出及び因子水準の設定
b)直交配列表の選定(必要な自由度の把握)と割り付け方法
c)分散分析表の各項目(S(平方和)、φ(自由度)、V(不偏分散)、F0(分散比))の意味合い
d)誤差分散(Ve)と母標準偏差の関係と値の妥当性
e)プーリングの原理とその可否判断